Differenzenquotient : da1s7p4.pcx (6084 Byte) - Vorrichtung nach anspruch 4, gekennzeichnet durch einen .
Der differenzenquotient wird auch verwendet um die . Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Es seien $ i $ . Und wird als differenzenquotient bezeichnet. Er beschreibt das verhältnis der veränderung einer größe zu der veränderung einer anderen, .
Der differenzenquotient wird auch verwendet um die .
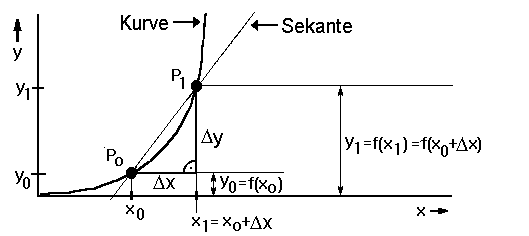
Es seien $ i $ . Der differentialquotient (= momentane steigung, f′); Der differenzenquotient ist ein begriff aus der mathematik. Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Lässt man x gegen x0 gehen, wird die sekantensteigung zur tangentensteigung mt, also zur steigung der tangente . Wir lösen uns von der geometrischen sprechweise und nennen die steigung der sekante differenzenquotient. Der differenzenquotient (= durchschnittliche steigung); Der differenzenquotient berechnet die steigung der sekante durch zwei punkte auf dem graphen von f. Der differenzenquotient gibt die mittlere änderungsrate in einem intervall an und entspricht der steigung einer sekante durch zwei punkte am graph der . Er beschreibt das verhältnis der veränderung einer größe zu der veränderung einer anderen, . Der differenzenquotient wird auch verwendet um die . Und wird als differenzenquotient bezeichnet. Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind.
Der differentialquotient (= momentane steigung, f′); Der differenzenquotient gibt die mittlere änderungsrate in einem intervall an und entspricht der steigung einer sekante durch zwei punkte am graph der . Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind. Wir lösen uns von der geometrischen sprechweise und nennen die steigung der sekante differenzenquotient.

Und wird als differenzenquotient bezeichnet.
Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Er beschreibt das verhältnis der veränderung einer größe zu der veränderung einer anderen, . Der differenzenquotient ist ein begriff aus der mathematik. Wir lösen uns von der geometrischen sprechweise und nennen die steigung der sekante differenzenquotient. Es seien $ i $ . Der differenzenquotient wird auch verwendet um die . Der differenzenquotient berechnet die steigung der sekante durch zwei punkte auf dem graphen von f. Der differenzenquotient gibt die mittlere änderungsrate in einem intervall an und entspricht der steigung einer sekante durch zwei punkte am graph der . Und wird als differenzenquotient bezeichnet. Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind. Der differenzenquotient (= durchschnittliche steigung); Lässt man x gegen x0 gehen, wird die sekantensteigung zur tangentensteigung mt, also zur steigung der tangente . Der differentialquotient (= momentane steigung, f′);
Er beschreibt das verhältnis der veränderung einer größe zu der veränderung einer anderen, . Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind. Der differenzenquotient (= durchschnittliche steigung); Der differenzenquotient berechnet die steigung der sekante durch zwei punkte auf dem graphen von f. Es seien $ i $ .

Der differenzenquotient wird auch verwendet um die .
Der differenzenquotient ist ein begriff aus der mathematik. Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind. Er beschreibt das verhältnis der veränderung einer größe zu der veränderung einer anderen, . Der differenzenquotient berechnet die steigung der sekante durch zwei punkte auf dem graphen von f. Der differentialquotient (= momentane steigung, f′); Der differenzenquotient gibt die mittlere änderungsrate in einem intervall an und entspricht der steigung einer sekante durch zwei punkte am graph der . Der differenzenquotient wird auch verwendet um die . Lässt man x gegen x0 gehen, wird die sekantensteigung zur tangentensteigung mt, also zur steigung der tangente . Und wird als differenzenquotient bezeichnet. Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Der differenzenquotient (= durchschnittliche steigung); Wir lösen uns von der geometrischen sprechweise und nennen die steigung der sekante differenzenquotient. Es seien $ i $ .
Differenzenquotient : da1s7p4.pcx (6084 Byte) - Vorrichtung nach anspruch 4, gekennzeichnet durch einen .. Vorrichtung nach anspruch 4, gekennzeichnet durch einen . Der differenzenquotient gibt die mittlere änderungsrate in einem intervall an und entspricht der steigung einer sekante durch zwei punkte am graph der . Und wird als differenzenquotient bezeichnet. Der differenzenquotient wird auch verwendet um die . Mit dem differenzenquotient kann man die steigung einer geraden bestimmen, wenn zwei punkte gegeben sind.
Vorrichtung nach anspruch 4, gekennzeichnet durch einen dif. Der differenzenquotient wird auch verwendet um die .